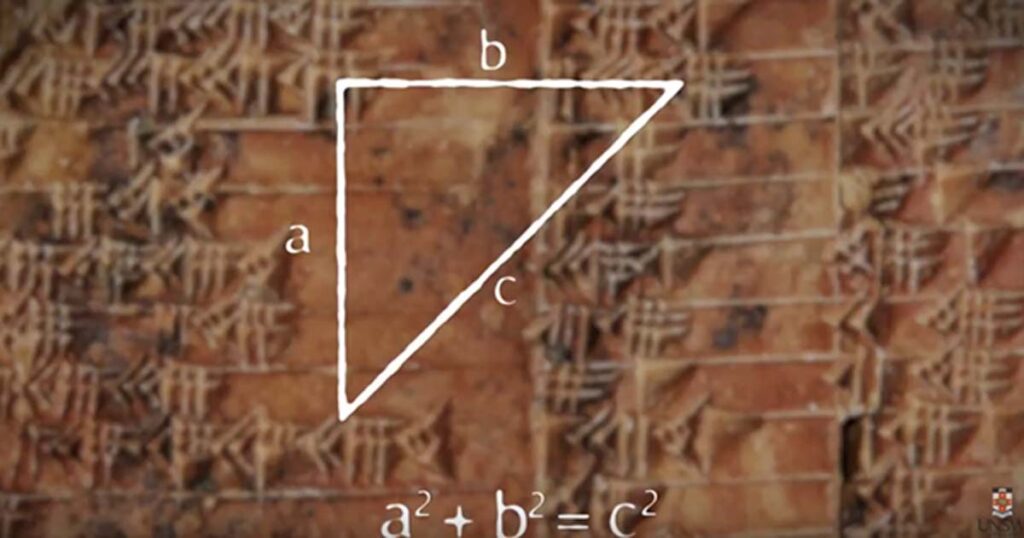Teorema di Pitagora.

 

Mi dispiace, Pitagora! Questa tavoletta babilonese di 3.700 anni fa (IM 67118) dimostra che il teorema di Pitagora era già matematica antica al tempo della sua nascita. Gli antichi scribi calcolarono c² quando la Grecia era ancora nell'età del bronzo! Il sistema numerico babilonese basato sul numero 60 regola ancora oggi i nostri orologi (60 minuti) e i nostri cerchi (360°): ecco un'influenza a lungo termine!
Nel 1770 a.C., un insegnante babilonese premette una canna nell'argilla bagnata per dimostrare come calcolare la diagonale di un rettangolo utilizzando quello che oggi chiamiamo teorema di Pitagora (a² + b² = c²). Una tavoletta ritrovata in Iraq contiene istruzioni matematiche dettagliate in base 60, il che dimostra che i Mesopotamici utilizzavano la formula 1.000 anni prima che Pitagora disegnasse il suo primo triangolo.
Ancora prima, la Tavoletta Plimpton 322 (circa 1800 a.C.) elenca le terne pitagoriche (ad esempio 3-4-5) in caratteri cuneiformi, il che suggerisce che si trattasse di un libro di testo per studenti avanzati. 

https://www.facebook.com/photo?fbid=1037443868487569&set=a.429428222622473

Teorema di Pitagora trovato su una tavoletta di argilla 1.000 anni più vecchia di Pitagora. - Hasan Jasim

 

Per chiunque abbia approfondito il mondo della matematica, il nome Pitagora probabilmente evoca sia ammirazione che occasionali sospiri esasperati. Sebbene Pitagora sia senza dubbio una figura monumentale nella storia della matematica, può sorprendere che l'equazione a lui più famosa, a² + b² = c², non sia stata una sua creazione. Invece, fu svelato secoli prima, inciso su un’antica tavoletta babilonese conosciuta come IM 67118, che precede Pitagora di un millennio.

Questo intrigante manufatto funge da testimonianza della profonda conoscenza matematica posseduta dai babilonesi, che utilizzavano il teorema di Pitagora per determinare la lunghezza di una diagonale all'interno di un rettangolo. Datata intorno al 1770 a.C., molto prima della nascita di Pitagora intorno al 570 a.C., questa tavoletta era probabilmente uno strumento didattico per l'insegnamento della matematica.

A rafforzare ulteriormente questa rivelazione è un'altra tavoletta del periodo tra il 1800 e il 1600 a.C. Adornate con un quadrato e triangoli, le iscrizioni della tavoletta, tradotte dal sistema di conteggio babilonese in base 60, rivelano una profonda comprensione del teorema di Pitagora, anche se non indicato con quel nome, così come di altri intricati concetti matematici.

Il matematico Bruce Ratner, nella sua ricerca su questo argomento, conclude: “I babilonesi conoscevano la relazione tra la lunghezza della diagonale di un quadrato e il suo lato: d = radice quadrata di 2. Questo fu probabilmente il primo numero conosciuto come irrazionale. Tuttavia, questo, a sua volta, significa che avevano familiarità con il Teorema di Pitagora – o, per lo meno, con il suo caso speciale per la diagonale di un quadrato (d² = a² + a² = 2a²) – più di mille anni prima. il grande saggio da cui prese il nome”.

Sorge allora la domanda: perché il teorema di Pitagora è stato attribuito a Pitagora? La risposta sta nella mancanza di scritti originali sopravvissuti dello stesso Pitagora. Gran parte della nostra conoscenza su di lui è stata tramandata attraverso i Pitagorici, i suoi seguaci e i membri di una scuola segreta da lui fondata nell'Italia meridionale, conosciuta come il Semicerchio di Pitagora. All'interno di questo ambito la conoscenza veniva trasmessa oralmente a causa della scarsità di materiale per scrivere. In segno di riverenza per il loro leader, molte scoperte fatte dai Pitagorici furono attribuite a Pitagora, dando vita infine al termine duraturo "Teorema di Pitagora".

Negli annali della matematica, le origini del teorema di Pitagora potrebbero essere avvolte nella notte dei tempi, ma l'eredità duratura degli antichi matematici babilonesi è una testimonianza della costante ricerca della conoscenza che abbraccia millenni.

https://www.facebook.com/photo/?fbid=741453221491906&set=gm.1503340893625406&idorvanity=141379536488222

Il teorema di Pitagora al tempo dei Babilonesi

I matematici greci hanno perso il primato dell’invenzione della trigonometria. Questo è il pensiero di Daniel Mansfield, ricercatore australiano che ha scoperto l’utilizzo di Plimpton 322, un’antica tavoletta babilonese in caratteri cuneiformi, famosa perché contiene una serie di numeri che da tempo facevano sospettare la conoscenza del teorema di Pitagora mille anni prima di Pitagora stesso. Il nuovo studio ha scoperto che si tratta della più antica tabella trigonometrica conosciuta. Le 15 righe sulla tavoletta descrivono una sequenza di 15 triangoli rettangoli di differente inclinazione e una serie di tavolette simili era probabilmente utilizzata dagli agrimensori e ingegneri dell’epoca per i loro calcoli. Oltre a essere la prima, è anche la tabella trigonometrica più accurata, grazie all’utilizzo di un particolare approccio matematico e ai calcoli in base sessagesimale, come quelli che utilizziamo per la misura del tempo e che evitano di avere resti. Un approccio geniale che secondo Mansfield può essere applicato anche oggi in vari campi, facendo tornare di moda la perduta scienza babilonese. Servizio di Stefano Parisini, Media Inaf Per approfondire: http://www.media.inaf.it/2017/08/24/p...