Un diario, dove annoto tutto ciò che più mi colpisce. Il mio blocco per gli appunti, il mio mondo.
mercoledì 29 gennaio 2025
"Il mito della Caverna" di Platone".
Scioccante! Le scoperte nascoste sotto le piramidi d'Egitto sfidano tutta la storia conosciuta. - Dany Pelati
Arrivata possibile spiegazione ad uno dei più grandi misteri della cosmologia. - Valerio Novara
Uno studio delle università di Bonn e St. Andrews propone una soluzione alla cosiddetta “tensione di Hubble”, un mistero della cosmologia.
L’universo si sta espandendo. La velocità con cui lo fa è descritta dalla cosiddetta costante di Hubble-Lemaitre. Ma c’è una controversia su quanto sia effettivamente grande questa costante: diversi metodi di misurazione forniscono valori contraddittori. Questa “tensione di Hubble” rappresenta un enigma per i cosmologi. I ricercatori delle Università di Bonn e St. Andrews propongono una nuova soluzione: utilizzando una teoria alternativa della gravità, la discrepanza nei valori misurati può essere facilmente spiegata. La tensione di Hubble scompare ed è uno dei misteri della cosmologia.
Cos’è la tensione di Hubble, mistero della cosmologia.
L’espansione dell’universo fa sì che le galassie si allontanino le une dalle altre. La velocità con cui lo fanno è proporzionale alla distanza tra loro. Ad esempio, se la galassia A è due volte più lontana dalla Terra rispetto alla galassia B, anche la sua distanza da noi cresce due volte più velocemente. L’astronomo statunitense Edwin Hubble fu uno dei primi a riconoscere questa connessione.
L’immagine mostra la distribuzione della materia nello spazio: i punti gialli rappresentano le singole galassie). La Via Lattea (verde) si trova in un’area con poca materia. Le galassie nella bolla si muovono nella direzione delle densità di materia più elevate (frecce rosse). L’universo sembra quindi espandersi più velocemente all’interno della bolla. Credit: Kroupa / University of Bonn.
A proposito di costante di Hubble. Secondo gli scienziati, la materia dovrebbe essere distribuita uniformemente nello spazio. Se così fosse, tuttavia, sarebbe difficile spiegare quali forze spingano le galassie alla loro elevata velocità. “Il modello standard si basa su una teoria della gravità avanzata da Albert Einstein“, affermano gli autori dello studio. “Tuttavia, le forze gravitazionali potrebbero comportarsi diversamente da quanto Einstein si aspettava”.

Svelata la foto che mostra gli atomi trasformarsi in onde quantistiche, come previsto da Schrödinger. - Valerio Novara
Grazie a una nuova tecnica, gli scienziati sono riusciti a catturare gli atomi di litio mentre si trasformano in onde quantistiche.
Per la prima volta in assoluto, i fisici hanno catturato un’immagine chiara dei singoli atomi che si comportano come un’onda. L’immagine mostra atomi fluorescenti che si trasformano in piccole “macchie” confuse di pacchetti d’onda ed “: è la dimostrazione del fatto che gli atomi esistono sia come particelle che come onde, uno dei capisaldi della meccanica quantistica.
La natura ondulatoria della materia.
“La natura ondulatoria della materia rimane uno degli aspetti più affascinanti della meccanica quantistica”, spiegano gli autori dell’articolo. Aggiungono che la loro nuova tecnica potrebbe essere utilizzata per immaginare sistemi più complessi, fornendo spunti su alcune questioni fondamentali della fisica. Proposta per la prima volta dal fisico francese Louis de Broglie nel 1924 e ampliata da Erwin Schrödinger due anni dopo, la dualità onda-particella afferma che tutti gli oggetti di dimensioni quantistiche, e quindi tutta la materia, esistono sia come particelle che come onde allo stesso tempo.
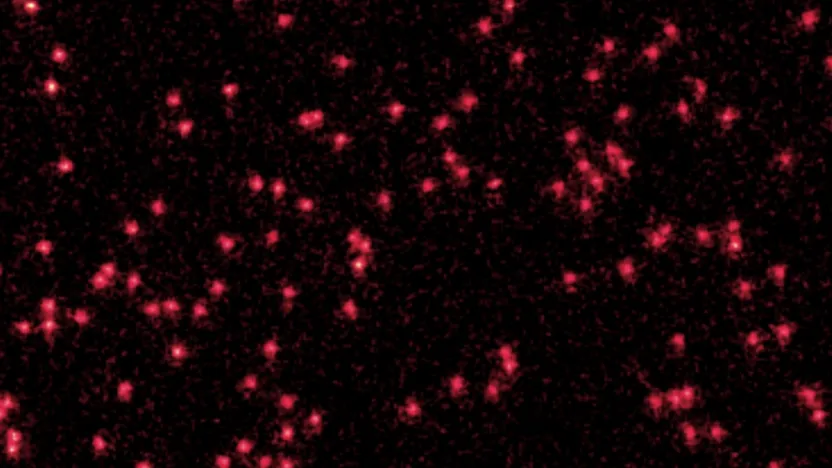
L’esperimento degli scienziati.
Con gli atomi raffreddati e confinati, i ricercatori hanno acceso e spento il reticolo ottico, espandendo gli atomi da uno stato confinato di quasi particella a uno simile a un’onda, e viceversa. Una telecamera al microscopio ha registrato la luce emessa dagli atomi nello stato di particella in due momenti diversi. Mettendo insieme le immagini, gli autori hanno ricostruito la forma di quest’onda e osservato come si espande nel tempo, in perfetto accordo con l’equazione di Schrödinger.
LA TRADUZIONE DELLE TAVOLE SUMERICHE.... - Ioana Mihaela Ilie
Il testo sumero rivela 8 esseri intelligenti che vennero sulla TERRA e governarono per 241.200 anni.
lunedì 20 gennaio 2025
Scoperta nella Regio IX di Pompei una sontuosa domus con terme private. - Mario Cardone
POMPEI. La casa romana (e pompeiana), come palcoscenico di una vita sontuosa e funzionale all’affermazione del rango sociale del dominus, costituiva un mezzo indispensabile all’arrampicata politica del medesimo, dal momento che l’accoglienza offerta agli ospiti doveva essere necessariamente opulenta per le famiglie patrizie, destinate per rango a gestire il potere, mentre i ricchi liberti la utilizzavano per affermarsi nel contesto pubblico.
Un grande complesso termale, rinvenuto all’interno di una domus privata pompeiana, annesso al suo sontuoso salone delle feste con banchetti, è emerso nel cantiere di scavo dell’insula 10 della Regio IX di Pompei. Si tratta, secondo gli esperti del Parco, di una delle maggiori terme domestiche pompeiane emerse sinora.
La sua vicinanza immediata al sontuoso salone nero di convivio attesta la funzione pubblica della casa privata di Pompei, in quanto è stata concepita come un palcoscenico sociale, pensato allo scopo di arricchire e consolidare rapporti di potere del suo dominus.
Le terme rinvenute, composte da calidarium, tepidarium, frigidarium e spogliatoio (apodyterium), accoglievano fino a trenta persone, a giudicare dalle panchine presenti nell’ultimo tra gli ambienti elencati. Di grande effetto figura la sala fredda, composta da una corte con una grande vasca interna.
Il commento nel comunicato del Parco sulla scoperta delle terme della Regio IX, site in prossimità alla sala da banchetto della domus, s’ispira al Satyricon di Petronio, in cui il ricco liberto Trimalcione aveva offerto una famosa cena ambientata in una città campana di I secolo d.C., non dissimile da Pompei, prima dell’eruzione del 79 d.C. Nel romanzo si narra che prima del banchetto i conviviali, incluso Trimalcione, si erano bagnati nelle terme.
La casa con edificio termale occupava la parte sud dell’insula 10, e doveva appartenere ad un personaggio di elevato rango sociale. Presenta le pareti decorate in II e III Stile, che dimostrano una storia familiare importante. Di sicuro, chi ne era il padrone l’aveva fatta allestire appositamente per ben figurare.
Le pitture di III stile conferiscono agli ambienti domestici l’atmosfera classica conferita dalla rappresentazione di tematiche della grecità mitica, tipica dell’otium aristocratico praticato all’epoca. Esprimeva influsso greco anche il peristilio con la grande vasca al centro, mentre il resto del complesso termale adiacente conferiva all’ambiente un rango da ginnasio greco, accentuato dalle scene atletiche successivamente apportate.
Si immagina che gli ospiti, a conclusione di un opulento e spettacolare banchetto, avrebbero sicuramente applaudito con ammirazione alla regia della magnifica iniziativa, orchestrata a meraviglia dal ricco padrone di casa e, dopo una serata incantevole trascorsa nel suo “ginnasio”, ne avrebbero parlato a lungo.
L’ingresso principale della domus esaminata era a sud. Qui era probabilmente collocato un atrio, dal quale si giungeva a un grande giardino con colonne che occupa quasi l’intera larghezza dell’isolato. Su un lato del peristilio si aprivano una serie di vani.
Da ovest a est: un grande oecus (soggiorno) decorato in II stile, un corridoio, un piccolo ambiente decorato in IV stile e un oecus corinzio, circondato da almeno 12 colonne su tre lati, con una megalografia di II stile con un fregio e con nature morte che rappresentano cacciagione e prodotti della pesca, probabilmente offerti in degustazione agli ospiti durante i banchetti.





